Merkle Tree, Merkle Proof
Block
Merkle Tree
머클 트리(Merkle Tree)는 비트코인의 '압축 알고리즘'이다.
블록(Block) 은 아래와 같이 되어있다.
- 블록 헤더 (Block Header): 블록의 신분증 역할을 하는 메타데이터(버전, 이전 블록 해시, 시간, 난이도, 머클 루트 등), 약 80 bytes
- 블록 바디 (Block Body): 실제 거래(Transaction) 내역들의 목록 (블록 바디에는 항상 최소 1개의 트랜잭션이 존재 (코인베이스 트랜잭션))
비트코인에서 블록 헤더는 정확히 80바이트이며, 다음 6개의 필드로 고정되어 있다.
| 필드 | 설명 |
|---|---|
| Version | 블록 버전 |
| Previous Block Hash | 이전 블록의 헤더를 해시한 값(체인 연결의 핵심) |
| Merkle Root | 블록 바디 내 모든 거래를 요약한 단 하나의 해시값 |
| Timestamp | 블록 생성 시간 |
| Bits | 난이도 목표값(압축 표현) |
| Nonce | 작업 증명(PoW)을 위해 대입하는 임의의 수 |
여기서 주목해야 할 점은 블록의 식별자인 '블록 해시'는 오직 블록 헤더만을 해시하여 생성된다는 점이다.
Block Hash = SHA256(SHA256(Block Header))
비트코인의 모든 거래 내역을 저장하려면 수백 기가바이트의 용량이 필요하다. 일반 사용자가 이를 모두 저장하기란 불가능에 가깝다. 사토시 나카모토는 비트코인 백서에서 "거래가 충분히 오래되어 확정되었다면, 디스크 공간을 절약하기 위해 실제 거래 데이터(바디)는 삭제(Pruning)할 수 있다" 고 언급했다.
'Pruned Node'(프루닝된 노드)는 블록체인 전체를 저장하지 않고, 오래된 블록 데이터를 삭제하여 디스크 공간을 절약하면서도 블록체인 검증과 보안에 참여하는 노드 유형이다. 이는 전체 노드(Full Node)보다 훨씬 적은 저장 공간을 차지하여 개인 사용자들이 더 쉽게 노드를 운영하게 해주며, 블록체인 네트워크의 탈중앙화와 보안에 기여하지만, 저장된 범위 밖의 거래는 확인할 수 없다는 특징이 있다.
여기서 중요한 점은 블록 해시는 블록안의 모든 거래(transaction)에 의존한다. 따라서, 거래가 하나라도 변경되면 블록 해시가 변경되고, 블록 헤더가 변경되어 작업 증명을 다시 해야 하는 상황이 발생한다.
이 문제(디스크 공간을 절약하고 블록의 해시를 깨지 않기 위해)를 해결하기 위해서 사용되는 자료구조가 Merkle Tree 이다. 머클 트리(merkle tree)의 핵심 아이디어는 "여러 데이터를 해시로 요약하고, 그 요약을 다시 해시한다" 이다.
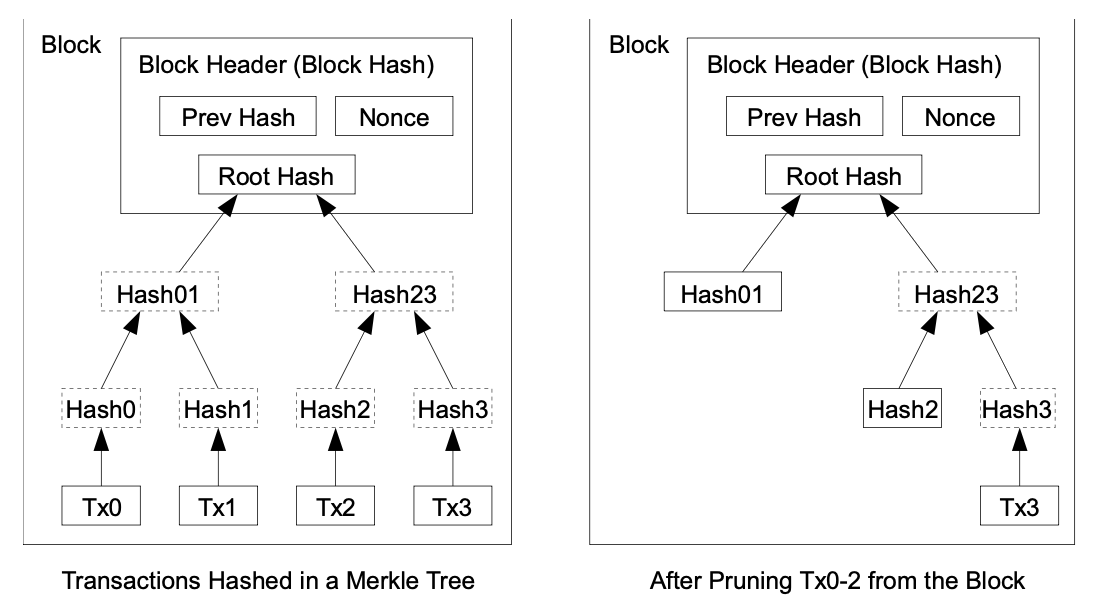
- 리프 노드(Leaf Node): 각 거래(Tx)를 해시한다. (Tx A → H(A))
- 내부 노드(Branch Node): 인접한 두 해시를 합쳐 다시 해시한다. (Hash(H(A) + H(B)))
- (Tip: 만약 거래가 홀수 개라면 마지막 거래를 하나 더 복사해서 짝을 맞춘다.)
- 루트 노드(Root Node): 최상단에 남은 단 하나의 해시값(Merkle Root)을 블록 헤더에 기록한다.
블록의 식별자 역할을 하는 것은 블록 헤더의 해시값이다. 이 헤더 안에는 거래의 요약본(해시값)인 머클 루트(Merkle Root)가 들어있다.
즉, 각 단계에서 Parent = SHA256(SHA256(left || right)) 이 과정을 반복하다보면 단 하나의 해시 값으로 블록내 모든 거래를 요약할 수 있다.
머클 트리를 사용함으로써 얻는 이점은 다음과 같다.
- 헤더와 바디의 분리 (Pruning 가능): 블록 헤더는 거래 전체가 아닌, 요약본인 머클 루트만을 포함한다. 따라서 아주 오래된 거래 데이터(바디)를 디스크에서 삭제하더라도, 블록 헤더의 내용은 변하지 않으므로 블록 해시와 체인의 연결은 깨지지 않는다.
- 위변조 감지 (Tamper Proof): 누군가 악의적으로 과거의 거래 내역을 단 1비트라도 수정하거나 삭제하면, 머클 루트 값이 완전히 바뀌게 된다. 이는 곧 블록 헤더의 변경을 의미하며, 해당 블록 이후의 모든 작업 증명을 다시 해야 하므로 사실상 조작이 불가능하다.
- 가벼운 검증 (SPV, Simplified Payment Verification): 특정 거래가 블록에 포함되어 있는지 확인하기 위해 블록 전체를 다운로드할 필요가 없다. 머클 경로(Merkle Path) 에 해당하는 몇 개의 해시값만 있으면, 루트 값과 대조하여 수 밀리초 안에 검증이 가능하다.
SPV - Simplified Payment Verification
SPV(Simplified Payment Verification)는 블록체인 전체를 다운로드 하지 않고도 특정 거래가 블록에 포함되어있는지 검증하는 방법이다. SPV 노드는 블록 헤더만 다운로드한다.
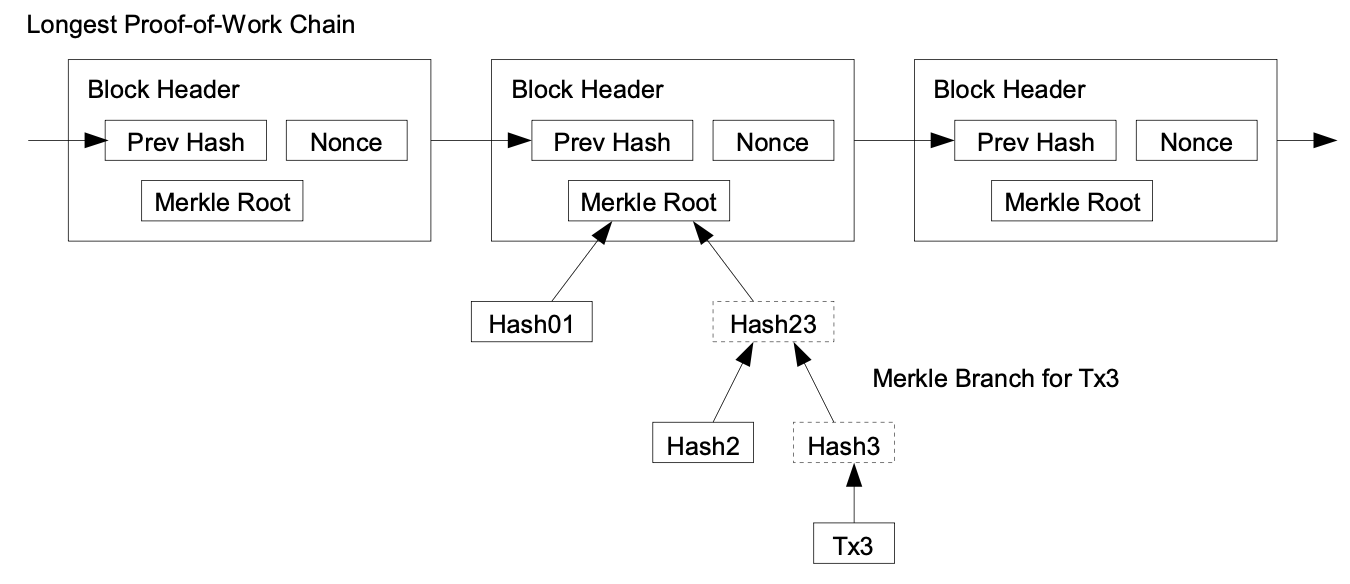
이해하기 쉽게 말하면, SPV 는 영수증(Tx) 하나를 확인하기 위해 백화점의 10년 치 장부(Blockchain)를 다 뒤지는 대신, 백화점 결재 도장이 찍힌 일일 마감표(Block Header)와 영수증 꾸러미(Merkle Path)만 확인하는 똑똑한 검증 방식이다.
SPV 노드가 "A가 나에게 1BTC 를 보냈다"는 거래(Tx)를 검증하는 과정은 다음과 같다.
- 헤더 동기화: SPV 노드는 네트워크의 풀 노드들에게서 가장 긴 체인의 블록 헤더들을 다운로드한다. (작업 증명 PoW 난이도를 통해 이것이 올바른 체인임을 확신한다.)
- 머클 경로 요청: 자신의 거래(Tx)가 특정 블록에 포함되어 있다는 증거를 풀 노드에게 요청한다. 이때 풀 노드는 전체 블록을 주는 게 아니라, 해당 거래의 '머클 경로(Merkle Path)' 만 제공한다.
- 루트 계산 및 비교:
- SPV 노드는 내 거래 해시 + 머클 경로 해시들을 계산한다.
- 계산 결과가 자신이 이미 가지고 있는 블록 헤더의 '머클 루트'와 일치하는지 확인한다.
- 검증 완료: 값이 일치하면, 수학적으로 이 거래는 해당 블록에 포함되어 있음이 증명된다. 이후 해당 블록 위에 몇 개의 블록이 더 쌓였는지(Confirmations) 확인하여 최종 승인한다.
SPV 노드가 풀 노드에게 "내 거래 내놔"라고 하면, 내 지갑 주소가 노출되어 프라이버시가 침해될 수 있기 때문에 이를 방지하기 위해 SPV 노드는 '블룸 필터(Bloom Filter)' 라는 확률적 데이터 구조를 사용한다. "정확히 이 거래를 줘"라고 하는 대신, "이런 패턴을 가진 거래들을 줘"라고 모호하게 요청하여 자신의 프라이버시를 지키면서 필요한 데이터를 받아온다. 블룸 필터는 확률적 자료구조(Probabilistic Data Structure)이다. 어떤 데이터가 특정 집합에 속해 있는지 아닌지를 매우 적은 메모리만 사용하여 빠르고 효율적으로 검사한다.
- "없음(No)" - 100% 확실함. (절대 거짓말하지 않음)
- "있을지도 모름(Maybe)" - 높은 확률로 있지만, 아닐 수도 있음. (False Positive 가능성 존재)
블록체인(특히 SPV 노드)에서는 데이터 검색 효율성과 사용자 프라이버시 보호라는 두 가지 핵심 문제를 해결하기 위해 사용된다.
SPV 노드가 자신의 지갑 주소들을 블룸 필터로 만들어서 풀 노드에게 보내는 예시를 살펴보자.
"이 필터(패턴)에 매칭되는 거래들만 보내줘."
- 프라이버시 보호: 블룸 필터는 해시 함수로 뭉개져 있고 '거짓 양성(False Positive)'이 섞여 있다. 풀 노드는 이 필터만 보고 사용자의 정확한 지갑 주소를 역추적하기 어렵다.
- 대역폭 절약: 풀 노드는 필터에 걸리는 거래만 추려서 보낸다. 이때 사용자의 진짜 거래뿐만 아니라, 우연히 매칭된(False Positive) 쓸모없는 거래도 일부 섞여서 온다.
- 최종 확인: SPV 노드는 받은 데이터 중에서 진짜 내 거래는 챙기고, 쓸모없는 거래(거짓 양성)는 로컬에서 버리면 된다.
Merkle Proof
머클 트리를 사용하면 블록 안에 담긴 수천 개의 거래르 모두 확인하지 않고도 "특정 거래(TXID)가 이 블록에 포함되어있는가?" 를 확실히 알 수 있다.
만약 2,000건의 거래가 담긴 블록에서 특정 거래 하나를 찾기 위해 모든 데이터를 다운로드해서 일일이 대조해야 한다면 엄청난 낭비일 것이다. 하지만 머클 트리는 전체 데이터를 몰라도, '머클 경로(Merkle Path)' 라고 불리는 몇 개의 해시값만 있으면 해당 거래가 집합의 일부임을 수학적으로 완벽하게 증명할 수 있다. 이는 데이터 전송량과 검증 시간을 획기적으로 줄여준다.
기술적으로 머클 트리는 "전체 집합(Set)을 노출하지 않고도, 특정 요소(Element)가 집합에 속해 있음(Membership)" 을 효율적으로 증명하는 방법(Merkle Proof)을 제공한다.
Merkle Proof:
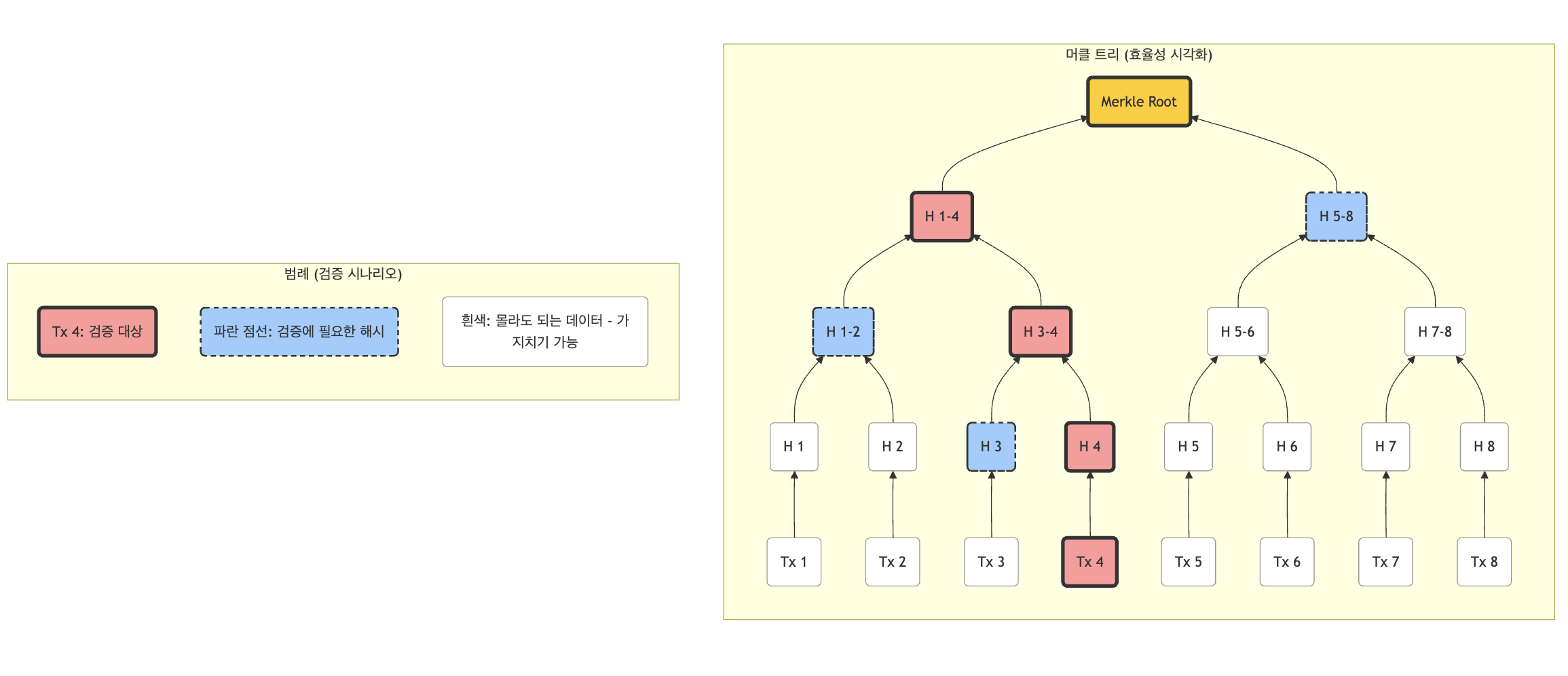
예를 들어 블록 하나에 2,048개의 거래가 포함되어 있다고 가정해 보자. 머클 트리가 없다면(O(N)) 특정 거래를 검증하기 위해 2,048개의 거래 데이터를 모두 받아 해싱해야 한다. 머클 트리가 있다면(O(log N)) 검증 대상 거래의 해시와 루트까지 가는 경로상의 해시값 11개(log_2 2048) 만 있으면 된다. 데이터의 크기가 커질수록 머클 트리의 효율성은 기하급수적으로 증가한다. 이것이 바로 모바일 기기 같은 경량 노드(Light Node)가 블록체인 네트워크에 참여할 수 있는 이유이다.