Recursion and Memoization
스택과 재귀, 자바와 코틀린에서의 꼬리 재귀
- Recursion
- Memoization
Recursion
Recursive Function
재귀 함수(Recursive Function)는 자기 자신을 다시 호출하는 함수를 의미한다.
public class Main {
public static void recursiveFunction() {
System.out.println("재귀 함수를 호출합니다.");
recursiveFunction();
}
public static void main(String[] args) {
recursiveFunction();
}
}
재귀 함수는 종료 조건이 무조건 있어야 한다. 그렇지 않으면 무한 루프에 빠질 수 있다.
public class Main {
public static void recursiveFunction(int i) {
// 100번째 호출을 했을 때 종료되도록 종료 조건 명시
if (i == 100) return;
System.out.println(i + "번째 재귀 함수에서 " + (i + 1) + "번째 재귀함수를 호출합니다.");
recursiveFunction(i + 1);
System.out.println(i + "번째 재귀 함수를 종료합니다.");
}
public static void main(String[] args) {
recursiveFunction(1);
}
}
재귀 함수는 내부적으로 스택(Stack)을 이용한다. 함수를 계속 호출했을 때 가장 마지막에 호출한 함수가 먼저 수행을 끝내야 그 앞의 함수 호출이 종료되기 때문이다.
컴퓨터 구조 측면에서 보자면 연속해서 호출되는 함수는 메인 메모리의 스택 공간(stack area)에 적재되므로, 재귀 함수는 스택 자료구조와 같다는 말은 틀린 말이 아니다.
재귀 함수를 이용하는 대표적인 예제로는 팩토리얼(Factorial) 문제가 있다.
Factorial
Factorial: n! > 1 x 2 x 3 x … x (n-1) x n
수학적으로 0! 과 1!은 1로 같다는 성질을 이용하여 n 이 1 이하가 되었을 때 함수를 종료하는 재귀 함수의 형태로 구현할 수 있다.
public class Main {
// 반복적으로 구현한 n!
public static int factorialIterative(int n) {
int result = 1;
// 1부터 n까지의 수를 차례대로 곱하기
for (int i = 1; i <= n; i++) {
result *= i;
}
return result;
}
// 재귀적으로 구현한 n!
public static int factorialRecursive(int n) {
// n이 1 이하인 경우 1을 반환
if (n <= 1) return 1;
// n! = n * (n - 1)!를 그대로 코드로 작성하기
return n * factorialRecursive(n - 1);
}
public static void main(String[] args) {
// 각각의 방식으로 구현한 n! 출력(n = 5)
System.out.println("반복적으로 구현:" + factorialIterative(5));
System.out.println("재귀적으로 구현:" + factorialRecursive(5));
}
}
재귀 함수를 사용했을 때의 장점은 코드가 더 간결해진다는 것이다. 이렇게 간결해진 이유는 재귀 함수가 수학의 점화식(재귀식)을 그대로 소스코드로 옮겼기 때문이다.
수학에서 점화식은 특정한 함수를 자신보다 더 작은 변수에 대한 함수와의 관계로 표현한 것을 의미한다. 이 개념은 다이나믹 프로그래밍을 배울 때 중요하다. 즉, 재귀를 사용할 생각이라면 점화식으로 표현할 수 있는지를 생각해보는 것이 좋다.
- Factorial 점화식
- n 이 0이거나 1일때 : factorial(n) = 1
- n 이 1보다 클 때 : factorial(n) = n x factorial(n-1)
특징
- 재귀 특징
- 스택 사용
- 점화식으로 표현 할 수 있어야 함
- 종료 조건 필수
Stack
재귀(Recursive)를 제대로 이해하는 것은 마냥 쉽진 않다. 일단 재귀가 스택(Stack)으로 동작한다는 것을 설명하기 위해 Factorial 구현을 예시로 들었다.
public class Recursive {
public int factorial(int n) {
System.out.println(Thread.currentThread().getName());
return n <= 1 ? 1 : n * factorial(n-1);
}
public static void main(String[] args) {
Recursive T = new Recursive();
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.println(T.factorial(n));
}
}
자, 재귀가 스택으로 동작한다는 것을 이해하기 위해선 다음과 같은 내용에 대해서 이해하고 있어야 한다.
- JVM 메모리 스택 영역
- 자바에서는 스레드가 생성 될 때 마다 스택 영역이 개별적으로 생성된다.
- 스레드가 메서드 호출 시, 지역변수, 매개변수 등이 저장된다.
- Heap 영역에 생성된
Object 타입 | 데이터의 참조 변수(Reference Variable)가 할당된다.- Ex. String ref = "abc";
-
실제로 Heap 영역에는 String "abc" 이런식으로 들어가고, ref 의 참조 변수가 stack 에 할당된다.
- 원시 타입의 데이터가 값과 함께 할당된다.
- 지역변수들은 scope 에 따른 visibility 를 가진다.
- 가장 마지막에 호출한 함수가 종료 되어야 이전에 호출한 함수들도 종료가 된다.
- JVM 메모리 힙 영역
- Heap 영역에는 주로 긴 생명주기를 가지는 데이터들이 저장된다. (대부분의 오브젝트는 크기가 크고, 서로 다른 코드 블럭에서 공유되는 경우가 많다.)
- 애플리케이션의 모든 메모리 중 stack 에 있는 데이터를 제외한 부분이라고 보면 된다.
- 모든 Object 타입(Integer, String, ArrayList, …)은 heap 영역에 생성된다.
- 몇개의 스레드가 존재하든 상관없이 단 하나의 heap 영역만 존재한다.
- Heap 영역에 있는 오브젝트들을 가리키는 레퍼런스 변수가 stack 에 올라가게 된다.
- 스택 자료 구조
- LIFO(Last In First Out)
- Call Frame(Call Stack)
- 재귀 함수는 함수가 호출될 때마다 Call Frame(호출 프레임)의 정보들이 스택 메모리에 저장된다.
- 호출 함수의 return address
- 스택에서 "가장 마지막에 호출한 함수가 종료 되어야 이 전에 호출한 함수들도 종료가 된다." 라고 했다. 호출 함수의 return address 가 있기에 돌아올 위치를 알 수 있는 것이다.
- 피호출 함수의 매개변수 와 지역변수
- 호출 함수의 return address
- 재귀 함수는 함수가 호출될 때마다 Call Frame(호출 프레임)의 정보들이 스택 메모리에 저장된다.
- 자바 스택과 힙 메모리 관리
자, 이제 위 코드의 입력(N) 값을 5로 주고 돌려보자.
결과는 다음과 같다.
main
main
main
main
main
120
호출된 재귀 함수들이 현재 main 스레드 위에서 동작하는 것을 볼 수 있다. (즉, 스레드가 현재 1개이다.) 그러면 위에서 배운 개념을 적용하면 생성된 스택 영역도 1개인 것이다.
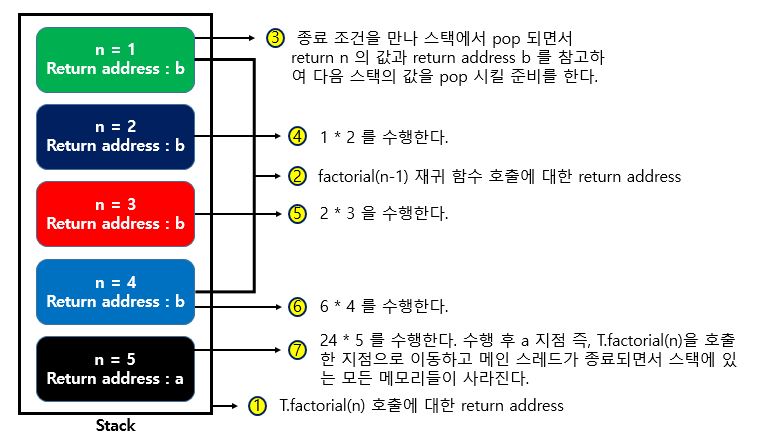
그림으로 스택과 재귀의 동작 과정을 살펴보자.
그림에서 색깔이 다른 이유는 다른 scope 를 의미한다. 따라서 스택에 n 이 값이 여러개 있더라도 scope 가 다르면 사용할 수 없다.
- 메인 스레드에 의해 factorial 함수가 호출되었으므로 return address (Ex. a)를 저장하고, 매개변수 n 과 원시 값을 저장한다. (n = 5)
- 스택 메모리의 특징에서 원시 값은 스택에 저장된다고 배웠다.
- 여기서 주소 값 a 는 T.factorial(n) 이 코드에 대한 주소 값이다.
- 다음으로 n 이 1이하가 아니므로 재귀 함수가 호출된다.
- 점화식이 호출되면서 새로운 return address (Ex. b) 값과 매개변수 n 과 원시 값을 저장한다. (n = 4)
- 여기서 주소 값 b 는 재귀 함수 호출에 대한 주소 값이다.
- 종료 조건인 n <= 1 이 될때 까지 반복하여 스택에 저장한다.
- 종료 조건을 만나 return 문을 호출하면서, 스택의 top 부분이 pop 되면서 return n 의 값과, return address 를 참고하여 다음 함수 호출 주소로 이동하여 계산할 준비를 한다.
- 메인 함수가 종료되면서 stack 에 있는 모든 메모리들이 사라진다.
재귀 함수의 문제: Stack Overflow
재귀 함수는 호출 시 마다 함수의 지역변수, 매개변수, 리턴 후 돌아갈 위치, 리턴 값 등을 스택에 저장한다. 따라서 무리하게 호출을 하다보면 스택 공간이 다 차버리는 스택 오버플로우(Stack Overflow) 현상이 발생할 수 있다.
Tail Recursion In Java
꼬리 재귀는 재귀 함수의 장점은 살리고, 단점을 보완하는 방법 중 하나이다.
- 꼬리 재귀 최적화를 위한 조건
- 재귀 함수를 꼬리 재귀 방식으로 구현할 것
- 컴파일러가 꼬리 재귀 최적화를 지원할 것
컴파일러가 꼬리 재귀 최적화를 지원하지 않는다면, 꼬리 재귀 방식으로 구현을 해도 일반 재귀 처럼 동작할 것이다.
꼬리 재귀는 재귀 호출이 끝나면 아무 일도 하지 않고 결과만 바로 반환되도록 하는 방법이다. 이 방식을 사용하면 이전 함수의 상태를 유지하지도 않고 추가 연산을 하지도 않아서 스택이 넘쳐나는 문제를 해결할 수 있게 된다.
꼬리 재귀 함수는 이름처럼 항상 함수의 꼬리부분(마지막)에서 실행되는데, return 되기 전에 값이 정해지며 호출당한 함수의 결과값이 → 호출하는 함수의 결과값 으로 반환된다.
- 꼬리 재귀
- 호출 당한 함수의 결과 > 호출한 함수의 결과
일반 재귀 방식의 코드를 다시 보자.
public int factorial(int n) {
return n <= 1 ? 1 : n * factorial(n-1);
}
일반적인 재귀의 경우 factorial(3)을 호출 했다고 하면 마지막에 호출된 재귀 함수 값이 1이면 그 값을 다음 스택에 넘겨서 2 * 1을 계산하게 하고, 그 결과를 또 다음 스택에 넘겨서 3 * 2 를 계산하게하여 결과를 도출한다. 일반 재귀의 마지막 부분은 아래처럼 생겼었다. factorial(n-1) 이 바로 호출당한 함수인데, 이 함수는 스택에 쌓였다가 빠져 나올 때 원래 자기 자리로 돌아가서 앞쪽의 n 과 곱해져야 한다. 즉, return address 가 필수이다.
위 코드에 대한 컴파일러의 해석은 동일하게 재귀 방식이다.
public int factorial(int n) {
return n <= 1 ? 1 : n * this.factorial(n - 1);
}
다음은 꼬리 재귀 방식이다.
public int factorialTail(int n, int total) {
return n == 1 ? total : factorialTail(n - 1, n * total);
}
public int factorial(int n) {
return factorialTail(n, 1);
}
꼬리 재귀의 핵심은 재귀 호출 이후 추가적인 연산을 요구하지 않도록 구현 하는 것이다.
꼬리 재귀의 마지막 부분을 보면 factorialTail(n - 1, n * total) 따로 연산 같은 작업을 추가로 하지 않고 반환만 한다. 따라서 굳이 자기 자리를 기억하지 않아도 된다. 즉, 스택에 return address 를 저장할 필요가 없어진다.
위 코드에 대한 (꼬리 재귀를 지원하는) 컴파일러의 해석은 다음과 같다.
int factorialTail(int n) {
int total = 1;
do {
if(n == 1) return;
total = total * n;
n = n - 1;
} while(true);
}
재귀호출은 사라지고, do-while 문을 이용하는 코드로 최적화되어 있는 것을 확인할 수 있다. 즉, 내부적으로 재귀 함수를 반복문으로 변경되어 실행이 된다. 따라서, Stack Overflow 에 대한 위험이 없다고 하는 것이다.
Java 와 꼬리 재귀 최적화
C++, C#, Kotlin, Swift 는 꼬리 재귀 최적화를 지원하며, JavaScript 는 ES6 스펙에서 지원한다고 한다. Scala 는 JVM 위에서 동작하는데, 꼬리 재귀 최적화를 지원한다고 한다. 하지만 Java 는 꼬리 재귀 최적화를 직접적으로 지원하지 않는다.
자바에서 진짜 최적화를 지원하지 않는지 테스트를 해보았다. 컴파일러의 해석 결과는 다음과 같았다.
public static int factorialTail(int n, int total) {
return n == 1 ? total : factorialTail(n - 1, n * total);
}
- 지원하지 않는 이유
- JDK 클래스에는 보안에 민감한 메소드가 있다고 한다. 이 메소드들은 메소드 호출을 누가 했는지 알아내기 위해 JDK 라이브러리 코드와 호출 코드간의 스택 프레임 갯수에 의존한다. 스택 프레임 수의 변경을 유발하게 되면 이 의존관계를 망가뜨려 에러가 발생할 수 있다.
- Java 에서 꼬리 재귀 사용하기
- Java 는 컴파일러 레벨에서는 직접적으로 꼬리 재귀 최적화를 지원하지는 않지만, Java 8의 람다식과 함수형 인터페이스(Functional Interface)로 꼬리 재귀와 같은 컨셉을 적용해볼 수 있다고 한다.
Java 8의 람다식과 함수형 인터페이스로 구현
package jungho.chapter5.factorial;
import java.util.Scanner;
import java.util.stream.Stream;
/**
* TailCalls Convenience Class
*/
class TailCalls {
public static TailCall call(final TailCall nextCall) {
return nextCall;
}
public static TailCall done(final int value) {
return new TailCall() {
@Override
public boolean isComplete() { // true 를 반환하여 재귀의 끝을 보고한다.
return true;
}
@Override
public int result() {
return value;
}
@Override
public TailCall apply() {
throw new Error("not implemented");
}
};
}
}
/**
* default 메서드를 이용하여 구현
*/
@FunctionalInterface
interface TailCall {
// 실행 대기 중인 다음 TailCall 인스턴스를 반환
TailCall apply();
// 단순히 false 를 반환 : false 라는 것은 아직 대기중이라는 의미가 된다.
default boolean isComplete() {
return false;
}
default int result() {
throw new Error("not implemented");
}
default int invoke() {
return Stream.iterate(this, TailCall::apply)
.filter(TailCall::isComplete)
.findFirst()
.get()
.result();
}
}
public class TailRecursiveWithLambda {
/**
* factorialTail() 메서드를 호출하면 TailCall 인스턴스와 함께 즉시 반환된다.
* 핵심 아이디어는 done() 메서드를 호출 하면 재귀가 종료 된다는 신호를 보낸다는 것이다.
* 반면에 call() 메서드를 사용하는 경우 재귀를 계속하도록 요청하지만 현재 스택 수준에서 한 단계 내려간 후에만 가능하다.
* @param n 입력값
* @param total 총 계산한 값
* @return TailCall
*/
public static TailCall factorialTail(final int n, final int total) {
if (n == 1) {
return TailCalls.done(total);
} else {
return TailCalls.call(() -> factorialTail(n - 1, n * total));
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.println(factorialTail(10, 1).invoke());
}
}
컴파일러가 해석한 결과는 다음과 같다.
public static TailCall factorialTail(int n, int total) {
return n == 1 ? TailCalls.done(total) : TailCalls.call(() -> {
return factorialTail(n - 1, n * total);
});
}
직접 디버깅을 하면서 Call Frames 를 확인해보면 알겠지만, 일반적인 재귀랑 다르게 하나의 스코프 안에서 n 과 total 의 값이 계산된다는 느낌을 받을 수 있다.
Debugging
Iterative Factorial
Recursive Factorial
Tail Recursive Not supports optimization in Java
Tail Recursive With Lambda and Functional Interface
Conclusions
- Tail Call 은 리턴 직전의 연산이 (재귀)함수 호출인 경우를 의미한다.
- Kotlin 의 Tail Call Optimization 은 컴파일러 레벨에서 지원되며, 그 결과 Stack Overflow 의 위험 없는 최적화된 코드가 만들어진다.
- Java 언어는 '아직' Tail Call Optimization 을 지원하지 않고 있으며, '언젠가는 지원하지 않을까?' 라는게 자바 아키텍트의 의견이다.
Tail Recursion In Kotlin
To implement a function in Kotlin using tail recursion, there is one rule to follow: the recursive call must be the very last call of the method.
코틀린에서 꼬리 재귀를 구현하기 위해서 지켜야하는 규칙이 있는데, 재귀의 호출이 함수의 마지막 호출이어야 한다.
Implementing Factorial
fun recursiveFactorial(n: Long) : Long {
return if (n <= 1) {
n
} else {
n * recursiveFactorial(n - 1)
}
}
- n 이 <= 1이면 n을 반환
- 누적 계산 = recursiveFactorial(n – 1)
- 반환 n * 누적
따라서 재귀 호출이 함수의 마지막 호출이 아니다.
Implementing Factorial as Tail Recursion
꼬리 재귀를 사용하여 재귀를 구현하려면 코드 일부를 수정해야 한다.
곱셈이 재귀 호출 이후가 아니라 재귀 호출 이전에 수행되었는지 확인해야한다.
fun factorial(n: Long, accum: Long = 1): Long {
val soFar = n * accum
return if (n <= 1) {
soFar
} else {
factorial(n - 1, soFar)
}
}
- 지금까지 계산 = n * 누적
- n <= 1 이면 soFar 를 반환
- 재귀 함수를 호출하고 n – 1 및 soFar 를 전달
올바른 형식의 재귀 함수가 있으면 tailrec 키워드 를 사용하여 꼬리 재귀를 고려하도록 Kotlin 에 지시 한다.
꼬리 재귀가 가능한 경우 함수를 반복문으로 다시 작성할 수 있음을 컴파일러에 알린다. 이 키워드는 함수 자체에 적용되므로 다음과 같이 된다.
tailrec fun factorial(n: Long, accum: Long = 1): Long
Compilation
꼬리 재귀의 목적은 스택 오버플로 문제를 피하기 위해 명령적 방식으로 실행되는 재귀 코드를 작성하는 것이다.
public final long factorial(long n, long accum) {
while(n > (long) 1) {
long var10000 = n - (long)1;
accum = n * accum;
n = var10000;
}
return n * accum;
}
꼬리 재귀는 반복문으로 컴파일되므로 Stack Overflow 의 위험이 전혀 없다.
Conclusion
tailrec fun factorial(n: Int, result: BigInteger = 1.toBigInteger()): BigInteger =
if (n <= 0) result else factorial(n - 1, result * n.toBigInteger())
fun main() {
println(factorial(5)) // 120
}
- 코틀린에서 꼬리 재귀를 사용하기 위해서는 재귀 호출이 함수 호출의 마지막이어야 한다.
- 꼬리 재귀 함수에 tailrec 키워드를 사용하면 컴파일러가 꼬리 재귀가 사용가능한 함수인지 먼저 판단한 다음, 반복문 형태의 코드로 컴파일하여 실행한다.
- 메서드 호출이 루프를 도는 것보다 더 많은 비용이 든다.
Memoization
자바에서 직접 꼬리 재귀를 사용하도록 구현하는 것은 힘들다라는 것을 느꼈을 것이다. 재귀를 사용하는 알고리즘에서 성능을 극대화 하는 방법 중 하나가 메모이제이션(Memoization)이라는 기법이 있다. 메모이제이션(Memoization)은 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술 이다. 동적 계획법(Dynamic Programming)의 핵심이 되는 기술이다.
이번엔 피보나치 수열(Fibonacci numbers)을 예시로 들어설명하겠다.
문제에서 요구하는 사항은 다음과 같다. 입력값 N 이 주어졌을 때 N 만큼의 피보나치 수열을 구하여 출력하라는 것이다.
피보나치 수열(Fibonacci numbers) : 앞의 2개의 수를 합하여 다음 숫자가 되는 수열
Input : 5
Output : 1 1 2 3 5
Step 1. 가장 간단한 코드
위에서 재귀를 사용하기 전에 점화식을 작성하라고 배웠다. 피보나치 수열의 점화식을 작성하면 다음과 같다.
- Fibonacci(n) = Fibonacci(n-2) + Fibonacci(n-1)
public class Main {
private static int n;
public static void main(String[] args) {
initializeInputData();
for (int i = 1; i <= n; i++) {
System.out.print(fibonacci(i) + " ");
}
}
private static void initializeInputData() {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
}
// 점화식 fibonacci(n) = fibonacci(n-1) + fibonacci(n-2)
// 종료 조건 n == 1 || n == 2
private static int fibonacci(int n) {
if(n == 1 || n == 2) {
return 1;
} else {
return fibonacci(n - 2) + fibonacci(n - 1);
}
}
}
Step 2. 피보나치 결과를 배열에 저장하고 반복하여 출력
public class MainTwo {
private static int n;
private static int[] fibonacciResult;
public static void main(String[] args) {
initializeInputData();
fibonacci(n);
for (int i = 1; i <= n; i++) {
System.out.print(fibonacciResult[i] + " ");
}
}
private static void initializeInputData() {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
fibonacciResult = new int[n + 1]; // 1 1 2 3 ... 따라서 0 번째 인덱스는 필요 없음
}
// 점화식 fibonacci(n) = fibonacci(n-1) + fibonacci(n-2)
// 종료 조건 n == 1 || n == 2
private static int fibonacci(int n) {
if(n == 1 || n == 2) {
return fibonacciResult[n] = 1;
} else {
return fibonacciResult[n] = fibonacci(n - 2) + fibonacci(n - 1);
}
}
}
위 코드의 단점은 시간이 오래 걸린다라는 것이다. 입력값 N 을 45 로만 줘도 한 4초가 걸린다. 위 코드를 메모이제이션 기법을 적용하여 1초 미만으로 줄여보겠다.
Step 3. 메모이제이션 적용
public class Memoization {
private static int n;
private static int[] fibonacciResult;
public static void main(String[] args) {
initializeInputData();
fibonacci(n);
for (int i = 1; i <= n; i++) {
System.out.print(fibonacciResult[i] + " ");
}
}
private static void initializeInputData() {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
fibonacciResult = new int[n + 1]; // 1 1 2 3 ... 따라서 0 번째 인덱스는 필요 없음
}
// 점화식 fibonacci(n) = fibonacci(n-1) + fibonacci(n-2)
// 종료 조건 n == 1 || n == 2
private static int fibonacci(int n) {
// Memoization 기법 사용 : 입력값 N 에 대한 결과가 존재하면 메모리에 들어있는 값을 재활용
if(hasResult(n)) {
return fibonacciResult[n];
}
// 재귀를 이용한 Fibonacci 계산
if (n == 1 || n == 2) {
return fibonacciResult[n] = 1;
} else {
return fibonacciResult[n] = fibonacci(n - 2) + fibonacci(n - 1);
}
}
// 처음에 배열이 0으로 초기화 되니까 0 보다 크면 이미 계산된 값이 존재한다는 의미
private static boolean hasResult(int n) {
return fibonacciResult[n] > 0;
}
}
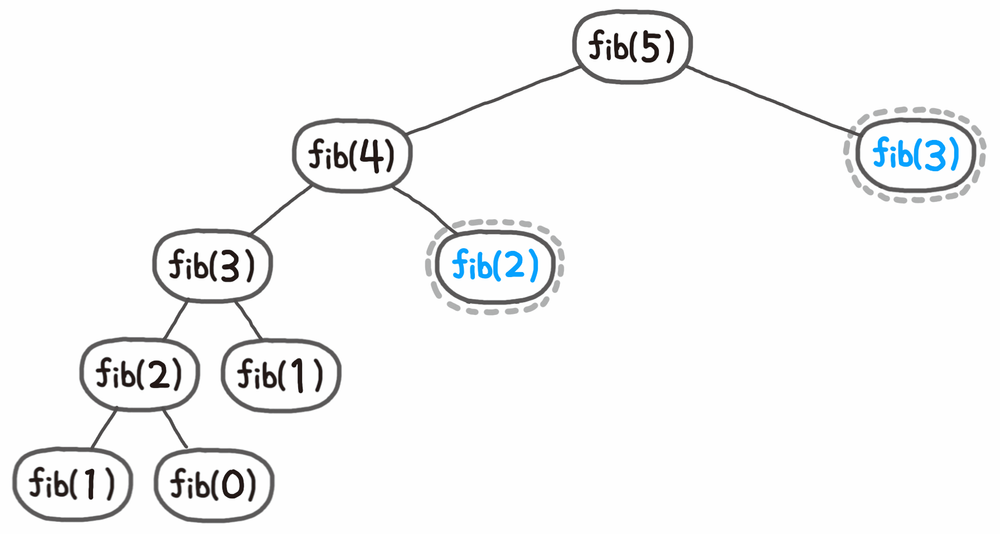
이미지 출처: Namu wiki
fibonacci(5) 를 호출하게되면 점화식에 의해 좌측으로 fibonacci(n - 1) 이 호출되며, 우측으로 fibonacci(n - 2) 가 호출된다. (코드 상으로는 사실 fibonacci(n - 1) + fibonacci(n - 2) 이렇게 되야 그림이랑 일치한다.) 우측편에서는 fibonacci(3) 까지만 호출되며 아래 노드들은 생기지 않는다. 지금은 5로 해놔서 그렇지만 입력 값이 1000 이상이 넘어간다고하면 많은 시간 절약을 할 수 있다.